O Número de Ouro e a Divina Proporção
- Balder
- 7 de jun. de 2017
- 5 min de leitura
O Número de Ouro e a Divina Proporção
1. Introdução
Existe um número na natureza que desde a antiguidade desperta a curiosidade e o fascínio de matemáticos e estudiosos. O número phi.2
Também chamado número de ouro, este misterioso número está por traz das construções da arquitetura clássica, das obras de arte do Renascimento e em diversos lugares da natureza, principalmente no corpo humano. Um número mágico, que organiza o universo em uma mesma proporção, a divina proporção.
Ao que tudo indica, a divisão áurea é conhecida desde os pitagóricos de 500 anos
a.C.
Eles sabiam da existência de somente cinco sólidos regulares que poderiam ser circunscritos por uma circunferência: o tetraedro, o cubo, o octaedro, o icosaedro e o dodecaedro. Este último ganhou atenção especial dos pitagóricos, pois suas faces são formadas por pentágonos regulares que estão repletos de segmentos áureos.
Seja o pentágono regular da figura 1. A interseção de duas de suas diagonais divide qualquer delas em média e extrema razão.
Ou seja,
2 Φ = 1,618034...

Figura 1. Pentágono regular

Através do pentágono os pitagóricos conheceram o pentagrama, ou triângulo triplo (figura 2). Acreditavam ser este, o símbolo da boa saúde, o emblema da perfeição. Esta admiração pelo pentagrama os fez escolher este para ser o símbolo da Sociedade de Pitágoras, e por esta insígnia, reconheciam os seus membros.
Figura 2. Pentagrama

2. Divisão áurea de um segmento
A divisão de um segmento em média e extrema razão é dada como se segue:
Seja um segmento de reta AB, dividido em dois segmentos pelo ponto C (figura 3).
Figura 3. Segmento AB dividido em proporção áurea

Podemos então escrever que
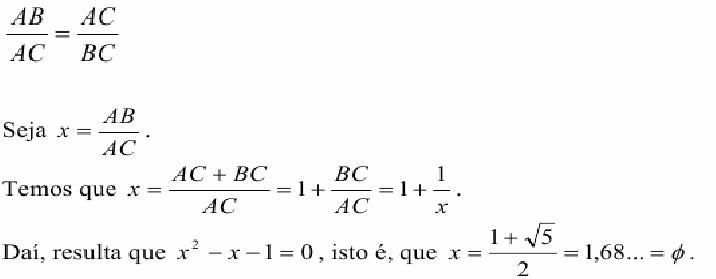
Chamamos a razão x de razão áurea.
Assim, o segmento AB está dividido em média e extrema razão, como era dito pelos matemáticos de antigamente. Kepler (1571-1630) denotou esta divisão de divina proporção.
Este problema de divisão de um segmento em razão áurea está solucionado no livro Elements3 de Euclides.
Mais tarde, Eudoxus, matemático grego, estudou a teoria das proporções e descobriu as propriedades de um retângulo que mais tarde ficaria conhecido como retângulo áureo, ou retângulo de ouro.
O retângulo áureo é um retângulo ABCD qualquer (figura 4) com a seguinte propriedade: se dele criarmos um quadrado, como ABFE, o retângulo restante, CDEF, será semelhante ao retângulo original ABCD. Sendo a + b e a os comprimentos dos lados do retângulo, cumpre-se a relação
O famoso livro de Euclides foi escrito por volta de 300 anos a.C.
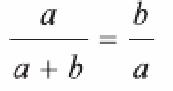
Figura 4. Retângulo áureo

O retângulo áureo tem muitas propriedades interessantes. Se desenharmos um retângulo de ouro, este pode ser dividido em um quadrado e em outro retângulo de ouro. Esse processo pode repetir-se infinitas vezes, mantendo-se a mesma proporção.
Para os gregos, o retângulo áureo representava a lei da beleza matemática. Ele está em sua arquitetura clássica e em suas esculturas. O Partenon, construído em Atenas por volta de 430-440 a. C. teve como base para a sua construção o retângulo de ouro (figura 5).
Sugeriu-se então no início do século passado que a letra grega phi, letra inicial do nome de Fídias, construtor e arquiteto do Partenon, fosse designada para representar o número áureo.
Muitos arquitetos que viveram depois de Fídias usaram o retângulo de ouro como base para suas construções arquitetônicas, como por exemplo, a Catedral de Notre Dame (figura 6).
Figura 5. Partenon

Figura 6. Catedral de Notre Dame

O retângulo de ouro também contém um espiral (figura 7) que repete as mesmas proporções da regra de ouro infinitamente.
Figura 7. Retângulo de Ouro

Encontramos este espiral nos lugares mais variados da natureza: microorganismos, flores, moluscos, chifres de animais e até mesmo nas galáxias. Por exemplo:
o tamanho dos espirais de um caracol aumenta com a proporção aproximada de 1,618;
o diâmetro dos espirais das sementes do girassol aumentam com uma proporção de aproximadamente 1,618;
Por volta de 1500, Leonardo da Vinci (1452-1519) também usou o que depois passaria a ser chamado de divina proporção em suas obras de arte. Como cientista, descobriu em cadáveres que o corpo humano obedece apenas uma proporção: a proporção áurea. Por exemplo:
meça sua altura e divida-a pelo comprimento de seu umbigo até o chão. O resultado será aproximadamente 1,6184;
meça o comprimento do seu braço e divida-o pelo comprimento do cotovelo até o dedo. O resultado será aproximadamente 1,618;
4 Devemos considerar erros de medida na régua ou na fita métrica, que são objetos acurados de medição.
a medida do seu dedo inteiro dividida pela medida da dobra central até a ponta, ou da dobra central até a ponta dividido pela medida da segunda dobra até a ponta resulta em aproximadamente 1,618;
o comprimento da perna inteira dividido pelo comprimento do joelho até o chão é aproximadamente 1,618;
a altura do crânio dividida pelo tamanho da mandíbula é 1,618.
Da Vinci constatou que nada na natureza obedece tanto a divina proporção quanto o corpo humano.
Existem pesquisas estatísticas atuais que revelam a presença da proporção divina em nosso corpo (Revista Odonto Ciência – PUCRS – dez 2006).
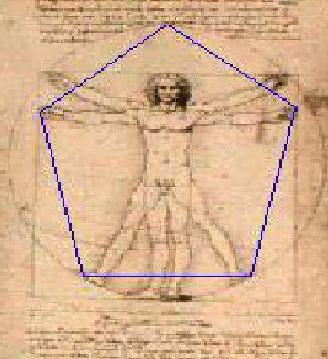
Luca Pacioli, matemático italiano, teve tal admiração por este número místico que por volta de 1509, escreveu um livro sobre as proporções divinas da natureza, chamado Divina Proportione, contendo ilustrações de Leonardo da Vinci. Entre estas ilustrações, estava o Homem Vitruviano (figura 9), que representa a perfeição e a beleza humana.
Figura 8. O Homem Vitruviano
3. Fibonacci e a mais famosa série matemática
No início do século XIII, o matemático Leonardo Fibonacci estudava o problema do crescimento populacional dos coelhos. A partir de dois coelhos, ele calculou como eles aumentavam a partir da reprodução de várias gerações, e se deparou com uma seqüência onde um número é igual a soma dos dois anteriores:
Esta é uma das séries mais famosas da matemática, conhecida como “Série de Fibonacci”.
Coincidentemente ou não, quando se vai fazer a divisão de cada termo pelo termo anterior, o resultado se aproxima do número phi. Quanto maior o termo, mais próximo do número de ouro a divisão estará.
Encontramos a sequência de Fibonacci naturalmente ao nosso redor:
a população de coelhos cresce seguindo os números de Fibonacci;
a maioria das flores tem 2, 3, 5, 8, 13, 21, 34, 55 ou 89 pétalas;
grande parte das espécies vegetais seguem a sequência de Fibonacci para a quantidade necessária de folhas a dar uma volta ao caule;
as ramificações da maioria das plantas cresce seguindo a sequência de Fibonacci.
O número de ouro instiga e fascina pesquisadores e curiosos há mais de vinte séculos. Até hoje, esta é considerada a mais perfeita proporção. Algumas pessoas descrevem que foi a beleza perfeita que Deus teria usado para fazer o mundo.
4. Referências
Huntley, H. E., A Divina Proporção – Um Ensaio sobre a Beleza na Matemática. Editora UnB, Brasília, 1985.
Pereira, G. M. R.; Câmara, M. A. da, O Pentagrama – FAMAT em Revista – número 07, p. 151-159. Setembro de 2006. Disponível em http: www.inf.unioeste.br/~rogerio. Acesso em 04/07/2008.
http: www.chabad.org.br/biblioteca/artigos/divina/home.html. Acesso em 09/07/2008.
http: www.pessoal.sercomtel.com.br/matematica/alegria/fibonacci/seqfib2.htm. Aces-so em 09/07/08.
http: www.digitalpaperweb.com.br/ezine/designe/o-que-e-proporcao-divina. Acesso em 09/07/2008.
http: www.members.tripod.com/caraipora/proporouro.htm. Acesso em 09/07/08.
http: www.perfeitauniao.org/oficina/2004/a_proporcao_aurea. Acesso em 09/07/08.
[8] http://revistaseletronicas.pucrs.br/ojs/index.php/fo/article/viewFile/1201/959 Acesso em
07/10/08.
[if gte vml 1]><v:shapetype id="_x0000_t75" coordsize="21600,21600" o:spt="75" o:preferrelative="t" path="m@4@5l@4@11@9@11@9@5xe" filled="f" stroked="f"> <v:stroke joinstyle="miter"></v:stroke> <v:formulas> <v:f eqn="if lineDrawn pixelLineWidth 0"></v:f> <v:f eqn="sum @0 1 0"></v:f> <v:f eqn="sum 0 0 @1"></v:f> <v:f eqn="prod @2 1 2"></v:f> <v:f eqn="prod @3 21600 pixelWidth"></v:f> <v:f eqn="prod @3 21600 pixelHeight"></v:f> <v:f eqn="sum @0 0 1"></v:f> <v:f eqn="prod @6 1 2"></v:f> <v:f eqn="prod @7 21600 pixelWidth"></v:f> <v:f eqn="sum @8 21600 0"></v:f> <v:f eqn="prod @7 21600 pixelHeight"></v:f> <v:f eqn="sum @10 21600 0"></v:f> </v:formulas> <v:path o:extrusionok="f" gradientshapeok="t" o:connecttype="rect"></v:path> <o:lock v:ext="edit" aspectratio="t"></o:lock> </v:shapetype><v:shape id="_x0000_s1026" type="#_x0000_t75" style='position:absolute; margin-left:98.5pt;margin-top:472.7pt;width:60.35pt;height:28.7pt;z-index:-1' o:allowincell="f"> <v:imagedata src="file:///C:\DOCUME~1\SILMA~1.AMA\CONFIG~1\Temp\msohtmlclip1\01\clip_image001.jpg" o:title=""></v:imagedata> </v:shape><![endif][if !vml][endif]




Comentários